AI Deep Dive 수학편

혁펜하임님의 강의를 들으면

 

미분 강의시간 고작 15분..!? 이라고 생각하시면 안됩니다;; ㅎㅎ
강의를 들으면 강좌 제목처럼 Deep Dive를 경험하게 됩니다..!

혁펜님의 수학 설명의 깊이를 체감함과 동시에,

강의를 일시정지 하며 처음 보는 깊이를 아이패드에 정리하면서 보다보면 어느세 30분이 지나있다는것을 체감하시게 됩니다..!

 

혁펜하임님이 오래 고민하시고 끓여서 걸쭉한 강의를 오마카세 해주시는걸 소화시키다 보면,

 

강의 한그릇 한그릇이 모두 진국임을 느끼게 됩니다..!

강사님께서 스토리 있는 딥러닝 요리를 만들지, 코스메뉴처럼 강의 목차를 어떻게 구성할지 많이 고민 한 게 느껴지는 명강의였습니다..!

 

수학 목차는 다음과 같습니다.

1	함수와 다변수 함수
2	로그 함수
3	벡터와 행렬
4	전치와 내적
5	극한과 입실론-델타 논법
6	미분과 도함수
7	연쇄 법칙
8	편미분과 그라디언트
9	테일러 급수
10	스칼라를 벡터로 미분하는 법
11	왜 그라디언트는 가장 가파른 방향을 향할까?
12	벡터를 벡터로 미분하는 법
13	벡터를 벡터로 미분할 때의 연쇄 법칙
14	스칼라를 행렬로 미분하는 법
15	행렬을 행렬로, 벡터를 행렬로 미분하는 법
16	랜덤 변수와 확률 분포
17	평균과 분산
18	균등 분포와 정규 분포
19	최대 우도 추정 (MLE)
20	최대 사후 확률 (MAP)
21	정보 이론 기초 (Entropy, Cross-Entropy, KL-divergence, Mutual information)

우선 함수와 다변수함수 1강 부터 6강 미분과 도함수 까지 강의 내용 요약은 다음과 같았습니다.

1. 함수와 다변수 함수

함수는 다음과 같이 표현이됩니다

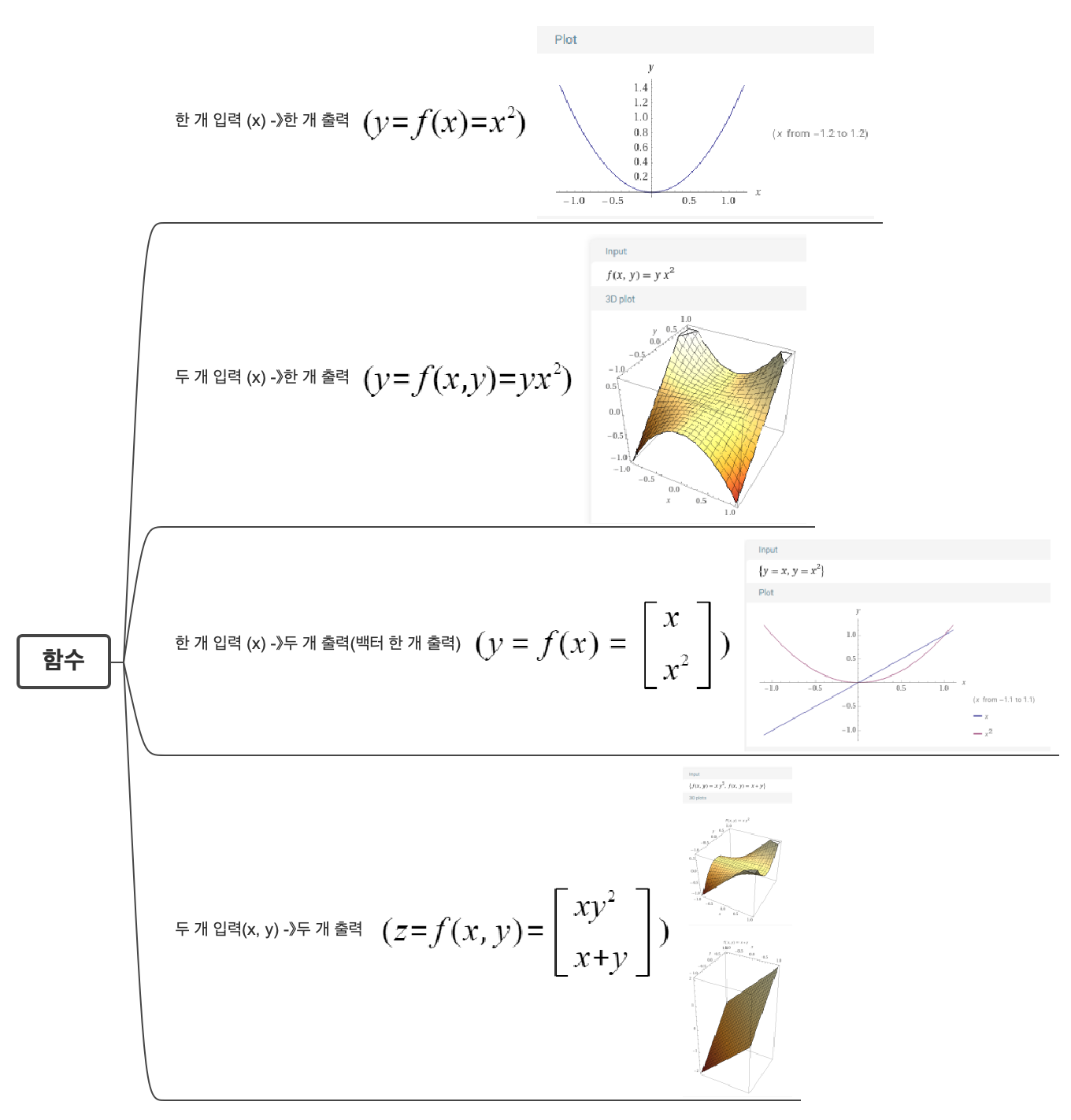
함수가 될 수 없는 케이스로, 입력 하나가 들어와서 한 입력이 2개 또는 여러개의 출력이 되는 경우는 함수가 아닙니다

 

2. 로그 함수

우리가 배웠던 로그 함수를 기억의 망각에서 다시한번 쉽게 오히려 더 이해가 잘 되게 로그 함수의 성질과 정의를 잘 정리해 주셨습니다

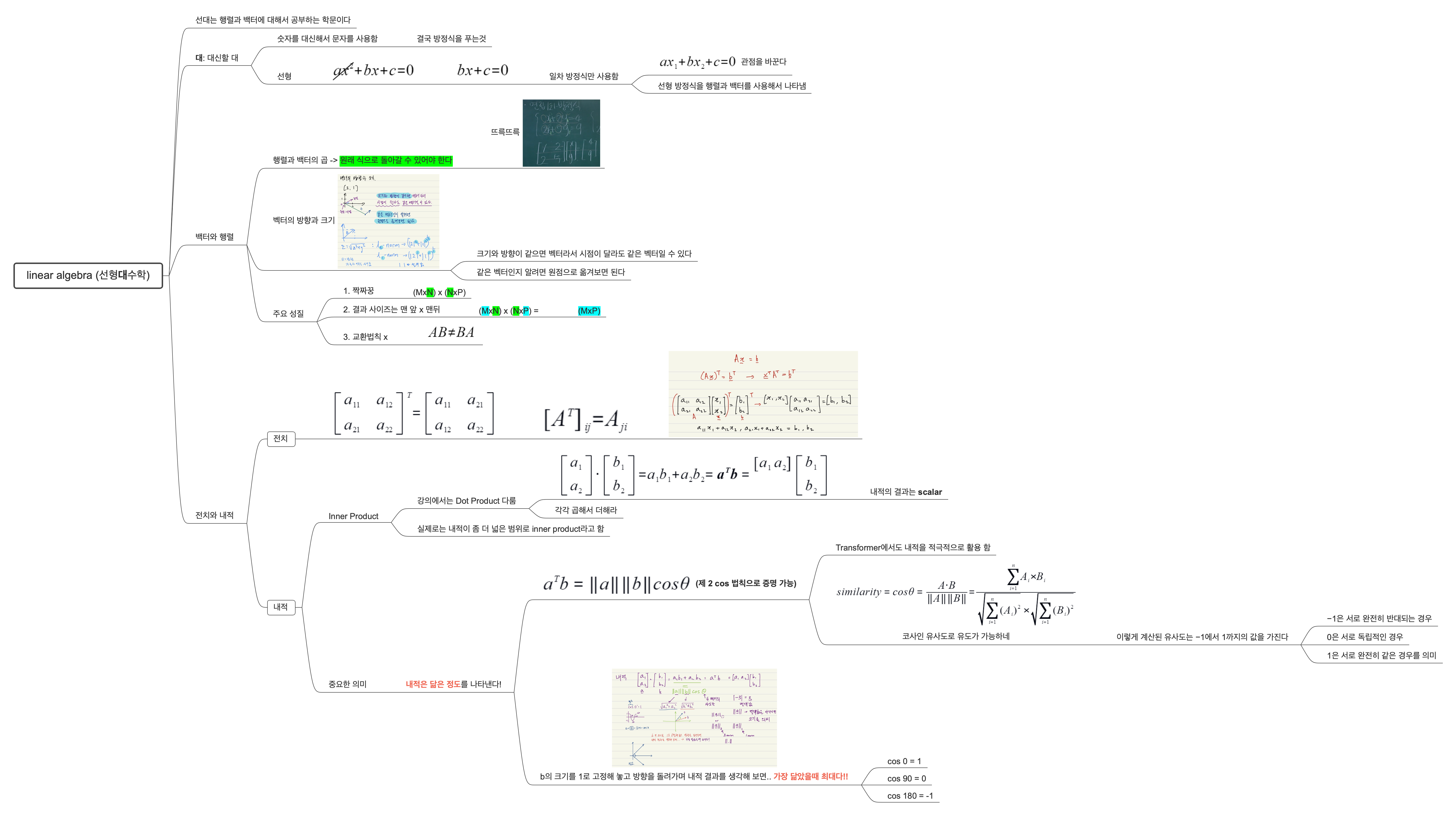
3. 벡터와 행렬 4. 전치와 내적

선형대수학의 기본을 다음과 같은 로직으로 복습해 주십니다~!

그래도 중요한건 반복적인 복습인거같아요.. 블로그를 쓰는 지금 설명하라 하면 다시 봐야만 할것같은 이 느낌..;;

그래도 AI Deep Dive 강의 소장하니 마음만 편하네요, 그런데 이런 느낌을 주의해야 한다고 알고 있습니다..!
그래서 전 혁팬님의 3일동안 진행하는 오프라인 강의 Deep AI Day를 통해 빨리 전체적으로 배운 뒤,

AI Deep Dive소장하는 강의로 계속 복습할 생각입니다~!

 

5. 극한과 입실론-델타 논법/ 6. 미분과 도함수 / 7. 연쇄 법칙 / 8. 편미분과 그라디언트

편미분과 그라디언트 까지 가기위해 준비된 오마카세였습니다

우선 미분의 의미를 알려면 극한에 대해서 알아야 합니다

왜냐하면 미분은 순간 변화율을 말하자는 건데, 극한의 정의를 모른다면, 순간이라는 단어가 어디서부터 어디까지 순간인 것인지 정의를 내릴 수 없기 때문입니다.

순간의 정의를 극한을 통해 안 뒤, 도함수를 통해 편리하게 미분하는 법을 배우고, 연쇄법칙을 통해 딥한 신경망을 보다 간편하게 계산할 수 있다는것을 깨우치게 되는 것이죠

마지막으로 딥러닝에서 가장 중요한 수학은 기울기 이죠~! (feat. 혁펜하임)

결론적으로 기울기는 각각의 함수에 대해서 편미분한 값을 벡터로 묶은것을 알 수 있게됩니다

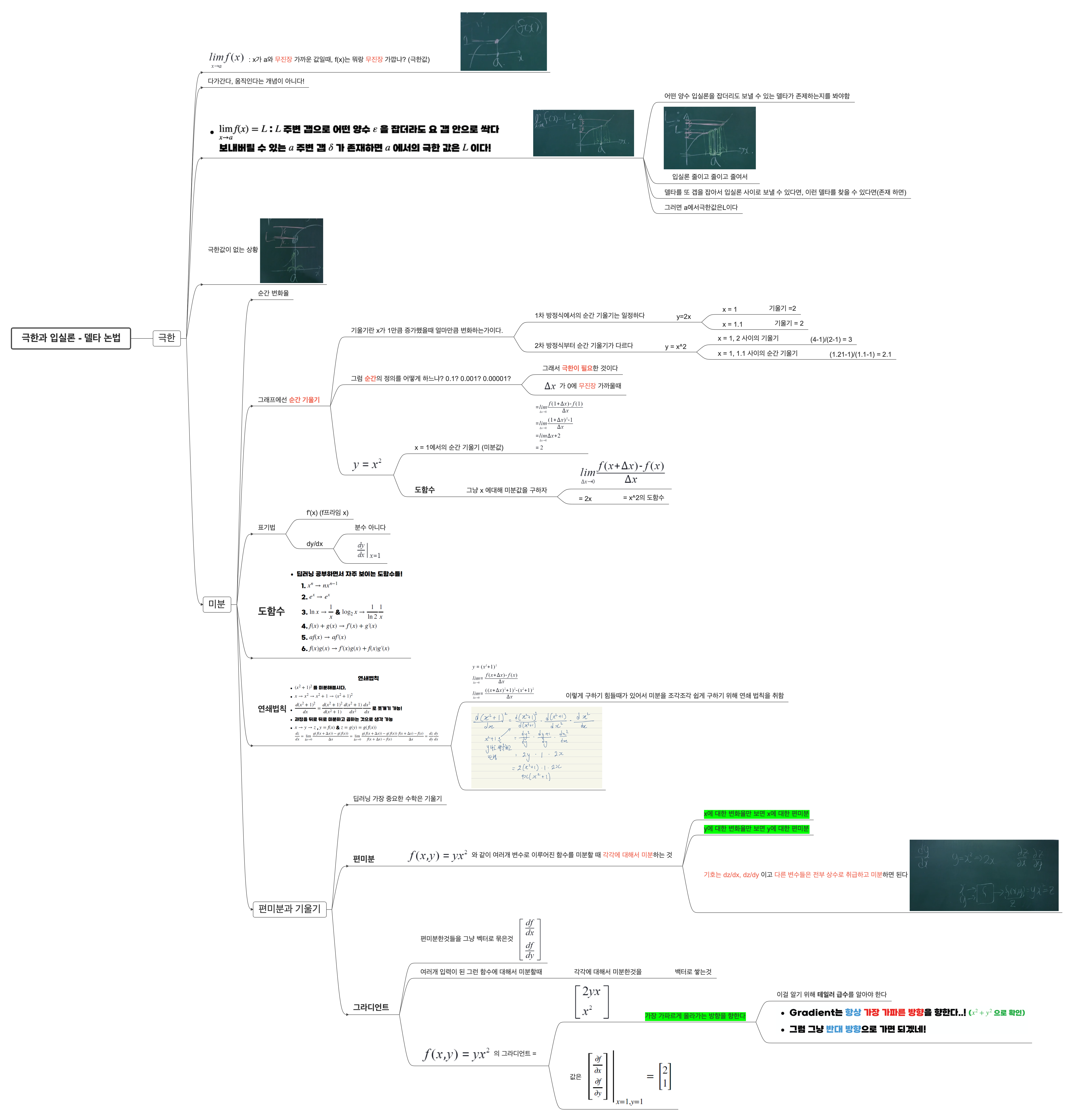
이제 기울기를 알았으니 테일러 급수를 통해, 기울기가 가파르게 올라가는 방향을 향한다는 성질을 알 수 있다고 합니다.

다음시간에.. 이어서 하도록 하겠습니다 ㅎㅎ

 

이렇게 혁펜하임님의 AI DEEP DIVE (fastcampus) 강의를 통해서 수학을 아래 단계부터 차근차근 격파하는 기분을 느낄 수 있게됩니다.

회사 다녀오면 피곤하고 졸리고.. 그리고 딥러닝 강의는 너도밤나무라 뭘 들어야 하는지 저또한 많이 찾아보고 책도 많이 사 보았는데요..;

저는 AI DEEP DIVE 하나면 현재 나와있는 기본 딥러닝 서적은 전~혀 살필요가 없다 라고 말할 수 있을것 같습니다.

 

바로 중급 난이도 이상의 책으로 넘어갈 수 있게 도움을 받을 수 있고, 또 이렇게 좋은 강의를 만들어주신 혁펜하임님의 수고와 노력에 진심으로 감사를 드립니다 :)